 |
Abstände zwischen vier Punkten
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
35. Vier Punkte sollen auf einer Ebene an unterschiedlichen Stellen platziert werden. Welche Möglichkeiten gibt es,
die vier Punkte so anzuordnen, dass es unter den sechs Abständen zwischen diesen Punkten nur zwei verschiedene gibt?
Möglichkeit 1:
Die einfachste und naheliegende Möglichkeit ist die, bei der die vier Punkte die Ecken eines Quadrates bilden. Hier sind die
vier Seiten und die zwei Diagonalen des Quadrats jeweils gleich lang.
Die Diagonalen sind dabei √2-mal, d.h. etwa 1,414-mal länger als die Seiten.
Möglichkeit 2:
Bei der nächsten Möglichkeit bilden die vier Punkte die Ecken eines Vierecks mit vier gleich langen Seiten, aber unterschiedlich langen
Diagonalen. Dieses Viereck ist demnach eine Raute. Die kürzere Diagonale hat dabei die gleiche Länge wie die Seiten der Raute.
Die längere Diagonale ist dann √3-mal, d.h. etwa 1,732-mal länger.
Möglichkeit 3:
Eine weitere Möglichkeit ergibt sich, wenn die vier Punkte ein konvexes Viereck bilden, bei dem jeweils zwei Seiten gleich lang sind.
Liegen die gleich langen Seiten einander gegenüber, dann entsteht ein Parallelogramm. Da hier mindestens eine Diagonale länger als jede
der längeren Seiten ist, gibt es hier keine Lösung. Liegen jeweils die gleich langen Seiten nebeneinander, handelt es sich um einen Drachen.
Hat der Drachen Diagonalen verschiedener Länge und ist die Länge der kürzeren Diagonale gleich der Länge der kürzeren Seiten des Drachens,
dann ist die längere Diagonale auf jeden Fall länger als die beiden längeren Seiten. Es ergibt sich auf diese Weise keine Lösung.
Allerdings erhält man eine Lösungsmöglichkeit, wenn die Länge der beiden Diagonalen gleich der Länge der beiden längeren Seiten ist.
Die beiden längeren Seiten des Drachens sind dann √(2 + √3)-mal, d.h. etwa 1,932-mal länger als die beiden kürzeren Seiten.
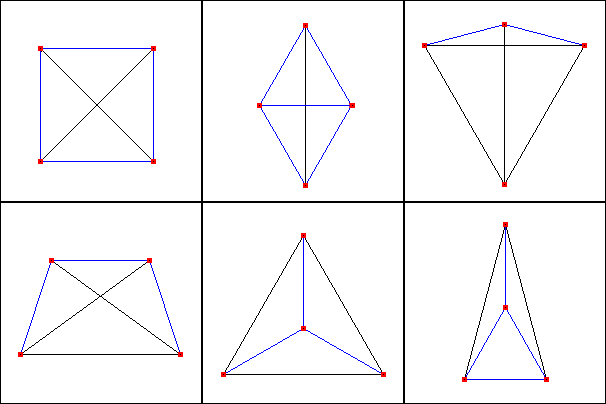
Möglichkeit 4:
Die vier Punkte können auch ein konvexes Viereck bilden, bei dem drei Seiten gleich lang sind. In jedem Viereck ist mindestens eine Diagonale länger
als die kürzeste Seite. Angenommen, die drei gleich langen Seiten sind länger als die vierte. Sind beide Diagonalen verschieden lang,
muss deswegen die kürzere Diagonale genauso lang wie die kürzere Seite und die längere Diagonale genauso lang wie die drei längeren Seiten sein.
Dann bildet die längere Diagonale zusammen mit zwei der längeren Seiten ein gleichseitiges Dreieck. Weil die kürzere Diagonale genauso lang ist
wie die kürzere Seite, muss der vierte Punkt auf der Mittelsenkrechten einer dieser beiden längeren Seiten liegen. Dabei entsteht kein konvexes Viereck.
Angenommen, die drei gleich langen Seiten sind kürzer als die vierte. Sind beide Diagonalen verschieden lang, muss deswegen die kürzere Diagonale
genauso lang wie die drei kürzeren Seiten und die längere Diagonale genauso lang wie die längere Seite sein. Dann bildet die kürzere Diagonale zusammen
mit zwei der kürzeren Seiten ein gleichseitiges Dreieck. Weil die längere Diagonale genauso lang ist wie die längere Seite, muss der vierte Punkt auf
der Mittelsenkrechten einer dieser beiden kürzeren Seiten liegen. Auch in diesem Fall entsteht kein konvexes Viereck. Sind beide Diagonalen gleich lang,
handelt es sich um ein Trapez. Die Länge der Diagonalen muss dann gleich der längeren Seitenlänge des Trapezes sein. Gibt es drei längere Seiten, dann
entstehen über der mittleren dieser drei Seiten zwei gleichseitige Dreiecke, die jeweils zusammen mit einer der beiden übrigen längeren Seiten und einer
der beiden Diagonalen gebildet werden. Das Trapez entartet dann zum gleichseitigen Dreieck. Deshalb kann es nur eine längere und drei kürzere Seiten geben.
Diese bildet jeweils zusammen mit einer benachbarten kürzeren Seite und mit einer Diagonalen ein gleichschenkliges Dreieck. Beide Dreiecke zusammen bilden
dann ein Trapez.
Das Längenverhältnis zwischen der längeren Seite und den drei kürzeren Seiten ist hier gleich dem Verhältnis des Goldenen Schnitts, also (1 + √5) / 2 = 1,618.
Möglichkeit 5:
Die vier Punkte können aber auch ein Dreieck bilden. Bei der einfachsten Möglichkeit sind drei der vier Punkte die Ecken
eines gleichseitigen Dreiecks. Der vierte Punkt liegt dann entweder auf einer der Seiten oder im Innern des Dreiecks. Die Abstände
zwischen diesem vierten Punkt und den drei übrigen Punkten sind in jedem Fall kleiner als die Seitenlänge des gleichseitigen
Dreiecks. Damit es insgesamt nicht mehr als zwei verschiedene Abstände gibt, muss der vierte Punkt zu allen anderen drei Punkten
den gleichen Abstand haben. Das ist nur dann erfüllt, wenn der vierte Punkt der Mittelpunkt des Dreiecks ist.
Die drei Seiten des Dreiecks sind bei dieser Lösung √3-mal, d.h. etwa 1,732-mal länger als die drei Abstände vom Mittelpunkt zu den Ecken des Dreiecks.
Möglichkeit 6:
Das Dreieck kann auch zwei verschiedene Seitenlängen aufweisen. Es handelt sich dann um ein
gleichschenkliges Dreieck. Die Abstände des vierten Punkts von den drei übrigen Punkten sind dann in jedem Fall kleiner als die längste
Seite des Dreiecks. Deshalb müssen diese drei Abstände gleich der kürzeren Seitenlänge sein. Hat das Dreieck zwei kürzere Seiten,
müssen diese beiden Seiten zusammen mit dem vierten Punkt jeweils ein gleichseitiges Dreieck bilden. Das geht nur, wenn der
vierte Punkt außerhalb des gleichschenkligen Dreiecks liegt, weil dieses Dreieck zwei Winkel kleiner als 60° hat. Dies ergibt
also keine Lösung. Falls nur eine kürzere Seite existiert, muss diese zusammen mit dem vierten Punkt ein gleichseitiges Dreieck bilden.
Und die Spitze des gleichschenkligen Dreiecks muss dann den gleichen Abstand zum vierten Punkt haben wie die Länge der kürzeren Seite.
Die längeren Seiten des Dreiecks sind dann √(2 + √3)-mal, d.h. etwa 1,932-mal länger als die kürzere Seite.
Schließlich können auch alle vier Punkte auf einer Geraden liegen. Die beiden äußeren Punkte haben aber jeweils
drei verschiedene Abstände zu den übrigen drei Punkten. Diese Anordnung ergibt also keine weitere Lösung.
Was ist verblüffend an diesem Mathematik-Rätsel? Viele glauben intuitiv, dass die naheliegende quadratische Anordnung die einzige
Lösung ist. Dann sind sie nicht nur verblüfft über die weiteren Lösungen, sondern auch über die vielen möglichen Anordnungen.
Sollen auf einer Ebene dagegen alle Abstände zwischen einer Anzahl von Punkten gleich sein, dann gibt es nur für zwei und drei Punkte
jeweils genau eine Lösung. Beide Lösungen sind sehr einfach. Bei zwei Punkten sind es die beiden Endpunkte einer Strecke und bei drei
Punkten die Eckpunkte eines gleichseitigen Dreiecks. Wenn die sechs Abstände zwischen vier Punkten gleich sein sollen, dann kann man
dafür z.B. auf einer Kugeloberfläche Lösungen finden. Man muss dann dort die vier Punkte so platzieren, dass sie die Eckpunkte
eines Tetraeders darstellen. Bei einem Tetraeder sind ja alle sechs Abstände zwischen seinen vier Eckpunkten gleich groß.
Und die Kugel ist hier die Umkugel des Tetraeders.
Wendet man diese Überlegung auf die Erde mit ihrem mittleren Radius von 6371 Kilometern an (mittlerer Umfang: 40.030 Kilometer),
dann müssen alle sechs Großkreisentfernungen zwischen den vier Eckpunkten des Tetraeders 12.173 Kilometer betragen. Da man
das Tetraeder beliebig drehen kann, findet man für die Lage der vier Punkte auf der Erdoberfläche unendlich viele Lösungen.
Deutlich interessanter wird die Sache, wenn sich alle vier Punkte an Land befinden sollen. Schließlich sind ja etwa 70%
der Erdoberfläche mit Wasser bedeckt.
Wer Lust hat, kann ja mal überlegen, ob es dafür überhaupt Lösungen gibt.
Falls ja, wäre ich an einer Beispiellösung interessiert!
Copyright © Werner Brefeld (2012)

