 |
Allgemeines Dreieck (möglichst schiefes Dreieck) für die Schule
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
22. Welches ist das schiefste Dreieck? Möglichst schief soll bedeuten, dass der Unterschied der
Innenwinkel des Dreiecks untereinander und zu den Winkeln von 0°, 90° und 180° maximal ist.
In der Schule soll man öfter ein Dreieck zeichnen, das möglichst wenig gleichseitig, gleichschenklig, rechtwinklig
oder schmal aussieht. Es soll so erreicht werden, dass beispielsweise eine Mittelsenkrechte, eine Winkelhalbierende und eine
Seitenhalbierende oder eine Höhe und eine Seite nicht fast zusammenfallen und dadurch die Zeichnung unübersichtlich wird.
Gesucht ist also ein allgemeines Dreieck, dessen Innenwinkel sich untereinander und von den oben genannten Winkeln
möglichst stark unterscheiden.
Für die folgenden Überlegungen soll der kleinste Winkel des Dreiecks α, der mittlere Winkel β und der
größte Winkel γ sein. Die Differenzen zwischen den Winkeln werden folgendermaßen definiert:
φ0 = α – 0° = α
φ1 = β – α
φ2 = γ – β
φ3 = 90° – γ für ein spitzwinkliges Dreieck
φ3 = γ – 90° für ein stumpfwinkliges Dreieck
φ4 = 180° – γ
Gesucht wird nun ein Dreieck, bei dem der kleinste der fünf Winkel φ0, φ1, φ2,
φ3 und φ4 möglichst groß ist.
Der Abstand des größten Winkels vom 180°-Winkel beträgt wegen der Winkelsumme im Dreieck von 180°:
φ4 = 180° – (180° – α – ß) = α + β > α
Wie man sieht, ist φ4 immer größer als φ0 und deshalb braucht der Unterschied zwischen γ und 180° nicht
weiter betrachtet zu werden.
Im Fall des spitzwinkligen Dreiecks sind alle Winkel kleiner als 90° und es gilt:
α + β + γ = (90° – φ3 – φ2 – φ1) + (90° – φ3 – φ2) + (90° – φ3) = 180°
φ1 = 90° – 2 · φ2 – 3 · φ3
Für ein vorgegebenes φ3 wird φ1 linear kleiner, wenn φ2 größer wird und umgekehrt.
Der kleinste von diesen beiden Winkeln ist also dann am größten, wenn beide Winkel gleich sind (φ1 = φ2):
φ1 = 90° – 2 · φ1 – 3 · φ3
φ1 = 30° – φ3
Wieder wird φ1 linear kleiner, wenn φ3 größer wird und der kleinste dieser beiden Winkel ist wieder dann am größten,
wenn sie beide gleich sind (φ1 = φ3):
φ1 = 30° – φ1
φ1 = 15°
Das Einsetzen von φ1, φ2 und φ3 ergibt:
α = 45°
β = 60°
γ = 75°
Weil der Unterschied des kleinsten Winkels zum 0°-Winkel gleich 45° und damit größer als 15° ist,
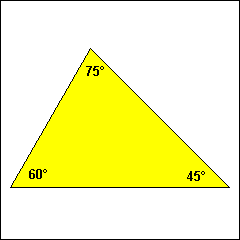
hat das schiefste spitzwinklige Dreieck die Innenwinkel 45°, 60° und 75°.
Hier noch eine anschauliche Erklärung: Man startet mit 60° für jeden Innenwinkel. Soll der Unterschied der drei Innenwinkel möglichst groß werden,
muss man einen Innenwinkel möglichst stark vergrößern und einen anderen im gleichen Maß möglichst stark verkleinern. Die Vergrößerung des einen
Innenwinkels kann man nur so weit durchführen, bis seine Abstände zu 90° und zum unveränderten 60°-Winkel gleich groß geworden sind. Das ist bei
75° der Fall. Der kleinste Innenwinkel hat dann entsprechend einen Wert von 45°.
Im Fall des stumpfwinkligen Dreiecks ist immer genau ein Winkel größer als 90° und es gilt:
α + β + γ = φ0 + (φ0 + φ1) + (90° + φ3) = 180°
φ1 = 90° – 2 · φ0 – φ3
Für ein vorgegebenes φ3 wird φ1 linear kleiner, wenn φ0 größer wird und umgekehrt. Der kleinste von diesen
beiden Winkeln ist also dann am größten, wenn beide Winkel gleich sind (φ0 = φ1):
φ0 = 90° – 2 · φ0 – φ3
φ0 = 30° – φ3 / 3
Wieder wird φ0 linear kleiner, wenn φ3 größer wird und der kleinste dieser beiden Winkel ist wieder
dann am größten, wenn sie beide gleich sind (φ0 = φ3):
φ0 = 30° – φ0 / 3
φ0 = 22,5°
Das Einsetzen von φ0, φ1 und φ3 ergibt:
α = 22,5°
β = 45°
γ = 112,5°
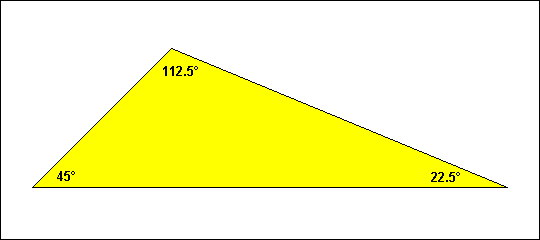
Das schiefste stumpfwinklige Dreieck hat also die Innenwinkel 22,5°, 45° und 112,5° und ist somit das schiefste Dreieck überhaupt.
Der Mindestabstand aller relevanten Winkeldifferenzen ist hier 22,5°.
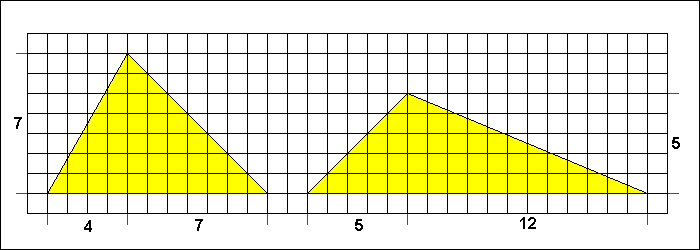
Wie die folgende Abbildung zeigt, lassen sich auf einer karierten Schultafel auf einfache Weise Dreiecke zeichnen,
die mit den oben erwähnten schiefen Dreiecken fast identisch sind. Zur Konstruktion des spitzwinkligen Dreiecks zeichnet man
dazu eine Strecke mit einer Länge von 11 Einheiten, errichtet 4 Einheiten vom linken Eckpunkt entfernt die 7 Einheiten lange Höhe
und verbindet dann die 3 Eckpunkte. Der mittlere Winkel hat hier einen Wert von arctan(7/4) = 60,26° und weicht, genauso wie
der größte Winkel mit seinen 74,74°, nur um 0,26° vom richtigen Wert ab. Noch besser wird das stumpfwinklige Dreieck angenähert,
weil hier der kleinste Winkel mit arctan(5/12) = 22,62° und der größte Winkel mit 112,38° nur um 0,12° falsch sind.
Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, ein möglichst allgemeines oder, etwas griffiger
ausgedrückt, ein möglichst schiefes Dreieck lasse sich nicht sinnvoll definieren und ein schiefstes Dreieck existiere
deshalb nicht.
Welche Werte ergeben sich mit den geforderten Randbedingungen für n-Ecke mit n > 3, also für Vierecke, Fünfecke, Sechsecke usw..?
Wenn man nur konvexe n-Ecke betrachtet, also n-Ecke, bei denen alle Innenwinkel kleiner als 180° sind, erhält man folgende Resultate für die innenwinkel:
Vierecke: 30°, 60°, 120°, 150° (Mindestabstand aller relevanten Winkeldifferenzen: 30°)
Fünfecke: 50°, 70°, 120°, 140°, 160° (Mindestabstand aller relevanten Winkeldifferenzen: 20°)
Sechsecke: 45°, 105°, 120°, 135°, 150°, 165° (Mindestabstand aller relevanten Winkeldifferenzen: 15°)
Siebenecke: 77,727°, 106,364°, 118,636°, 130,909°, 143,182°, 155,455°, 167,727° (Mindestabstand aller relevanten Winkeldifferenzen: 12,273°)
Achtecke: 100°, 110°, 120°, 130°, 140°, 150°, 160°, 170° (Mindestabstand aller relevanten Winkeldifferenzen: 10°)
Neunecke: 108°, 116°, 124°, 132°, 140°, 148°, 156°, 164°, 172° (Mindestabstand aller relevanten Winkeldifferenzen: 8°)
n-Ecke mit n >= 8: 180° - n · 720° / (n·(n+1)), 180° - (n-1) · 720° / (n·(n+1)), ...,
180° - 1 · 720° / (n·(n+1)) (Mindestabstand aller relevanten Winkeldifferenzen: 720° / (n·(n+1)) )
Links zum Thema:
Jürgen Köller: Allgemeines Dreieck
Copyright © Werner Brefeld (2005)



